GNN-DQN; Optimization of (Dynamic) Vehicle Routing for Waste Collection in Smart Cities

Abstract

This study presents a Graph Neural Network (GNN) and Deep Q-Network (DQN)-based framework to optimize waste vehicle routing in smart cities. The GNN processes graph-structured data to extract spatial features, while the DQN dynamically determines the optimal routes. The proposed model minimizes travel distances, avoids revisits, and reduces operational costs and carbon emissions. Experimental results show significant improvements, with travel distances reduced by 31% and rewards increasing steadily. This framework provides a scalable and intelligent solution for efficient waste collection, contributing to more sustainable urban waste management systems. Future work includes dynamic traffic integration and multi-vehicle optimization.

Introduction

Environmental concerns about the waste problem in cities have been growing with the rapid acceleration of urbanization and global growth of population. On average, a citizen in a developed country produces around half a ton of waste per year.¹ Considering that in a metropolitan area, there are at least 100,000 residents, that makes 50,000 tons of waste annually. Although the population growth occurs very rapidly, the collection and transportation methods of waste are often outdated.² Collection costs account for about 40 to 60 percent of a community’s solid waste management costs³, which shows the dire need for more current, updated methods of efficient waste management. Not only accounting for the waste of fuel and resources regarding human labor, but also there is a problem of carbon emission and its impact in the atmosphere. Optimizing routes could lead to reduction of 4.2-12 kg CO2 per ton of waste on average⁴. This will benefit both the waste management facilities and all the city residents.

Related Work

The routing optimization problem has long been long explored, starting with the Traveling Salesman Problem (TSP), Vehicle Routing Problem(VRP), and to the Collection Vehicle Routing Problem of Garbage Facilities (CVRPGF). Route optimization for waste vehicles was first introduced by Beltrami and Bodin in 1974, and since then, various algorithms have been implemented. Among classic algorithms, Norhafezah et al. uses Dijkstra’s algorithm to plan and simulate the optimized waste collection routes.⁵ In approaches utilizing machine learning models, Liang et al. applied ant colony optimization, simulated annealing, genetic algorithm, and other techniques to compare their performances.⁶

I will implement Graph Neural Networks (GNN) combined with Deep Q-Learning (DQN) to solve the Collection Vehicle Routing Problem of Garbage Facilities (CVRPGF). GNNs, which operate on graph-structured data, will represent city road networks and waste collection points efficiently, allowing the model to learn from the structure and connectivity of the road network itself. Deep Q-Learning (DQN), as a reinforcement learning algorithm, enables the agent to explore and exploit its environment, learning an optimal routing policy through interactions. DQN dynamically updates the current state of the vehicle, road conditions, and other relevant elements to make informed routing decisions. The GNN-DQN framework has proven to be effective for solving dynamic routing problems, reducing travel time, and optimizing waste collection efficiency.

Methodology

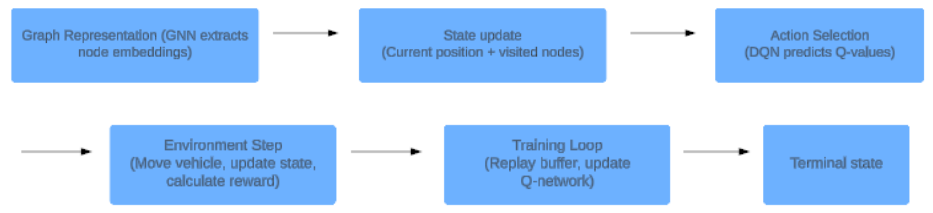
The Collection Vehicle Routing Problem of Garbage Facilities (CVRPGF) is formulated as a Markov Decision Process (MDP) with multiple states, actions, a transition function, and rewards. States represent the position of the vehicle (current node) and the set of visited nodes in the city graph. This is encoded as a combination of a one-hot vector (current position) and a binary vector (visited nodes). Actions represent the vehicle’s moves from the current node to its neighboring nodes in the graph. The transition function updates the state by moving from one node to another, adding the visited node to the set, and calculating a cost based on the edge weight, which is the travel time of the vehicle. There are negative and positive rewards. Negative rewards are given when a vehicle fails to completely empty a trash bin or chooses a longer path by revisiting nodes with empty trash bins. Positive rewards are given when a bin is emptied completely and when all bins are empty, completing its task. As all the trash bins are emptied and the vehicle returns to the facility, it reaches the terminal state.

This study utilizes GNN-DQN to optimize vehicle routing, using both graph-structured data and reinforcement learning to solve CVRPGF. A GNN is employed to process this graph and extract meaningful node embeddings. These embeddings encode the spatial relationships between nodes and provide rich features that reflect the graph structure. The GNN consists of graph convolutional layers, which aggregate information from neighboring nodes to update the node representations. Mathematically, the node embedding at layer 𝑘 is updated as:

$$ h_i^{(k+1)} = \mathrm{ReLU}\left( W_k \sum_{j \in \mathcal{N}(i)} h_j^{(k)} + b_k \right) $$ where \( h_i^{(k)} \) is the node feature at layer \( k \), \( W_k \) is the learnable weight matrix, and \( \mathcal{N}(i) \) represents the neighboring nodes of \( i \).

Using the GNN-extracted node embeddings as input, this study employs a Deep Q-Network (DQN) to train the agent and make routing decisions. The DQN is effective in handling large state-action spaces. First, the states are initialized and serve as the input to the network. During action selection, the DQN predicts Q-values for all possible actions, calculating the expected rewards for each action. The agent may exploit by selecting the action with the highest Q-value or explore other options based on an ε-greedy strategy. After selecting an action, the agent moves to the chosen node, updates the state, incurs a cost, and receives a reward. Training is facilitated through a replay buffer, where transitions (state, action, reward, next state) are stored. The Q-network is updated by sampling mini-batches from the buffer to minimize the loss:

$$ \mathcal{L} = \mathbb{E}\left[ \left( r + \gamma \max_{a'} Q'(s', a') - Q(s, a) \right)^2 \right] $$ where \( Q \) is the current network, \( Q' \) is the target network, \( r \) is the reward, and \( \gamma \) is the discount factor. When all the following steps occur and the task is finished by emptying all the trash bins and the vehicle returns to the facility, it reaches terminal state.

Results

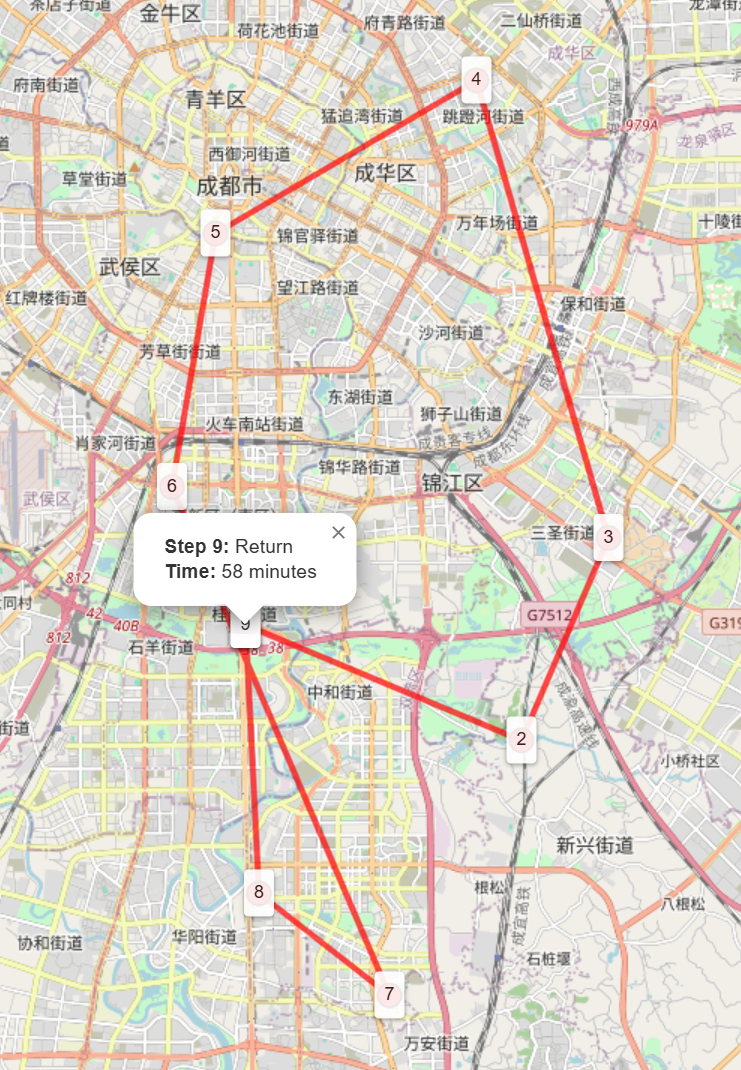
The experiment was conducted using a custom Gym environment to simulate garbage collection routing. The environment was modeled as a graph, where nodes represent waste collection points, and edges represent the roads between them. Each edge was assigned a weight corresponding to the travel time or distance. The state includes a one-hot encoded current position of the vehicle and a binary vector indicating visited nodes. A negative reward was assigned for distance traveled and revisiting nodes, while a positive reward was granted for successfully visiting all nodes, as mentioned above. The training parameters for GNN-DQN are 1) episodes: 1000, 2) batch size: 64, 3) discount factor: 0.99, 4) learning rate: 0.001, and 5) Epsilon decay: 0.995 with a minimum value of 0.1. For evaluation metrics, the total reward, total distance traveled, and number of revisits were measured.

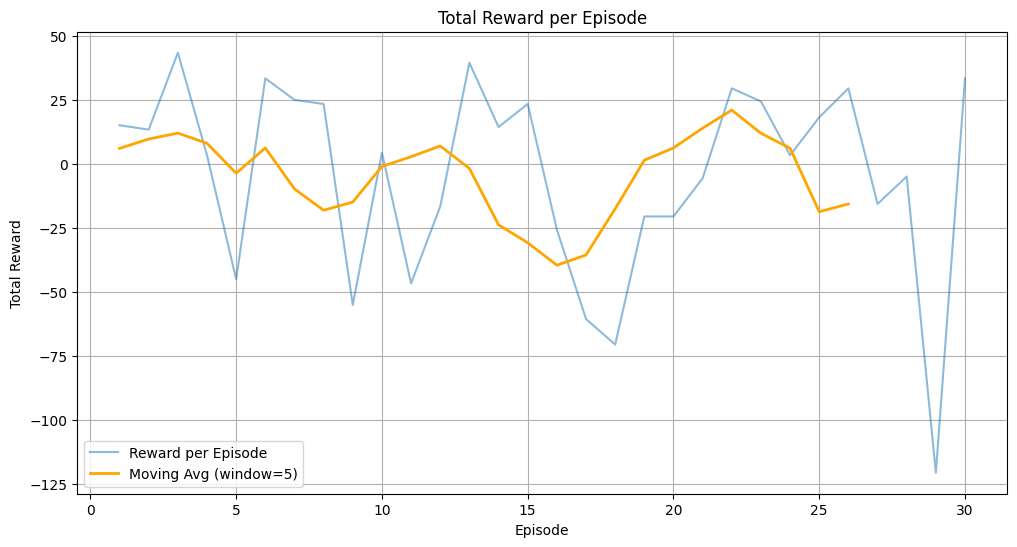
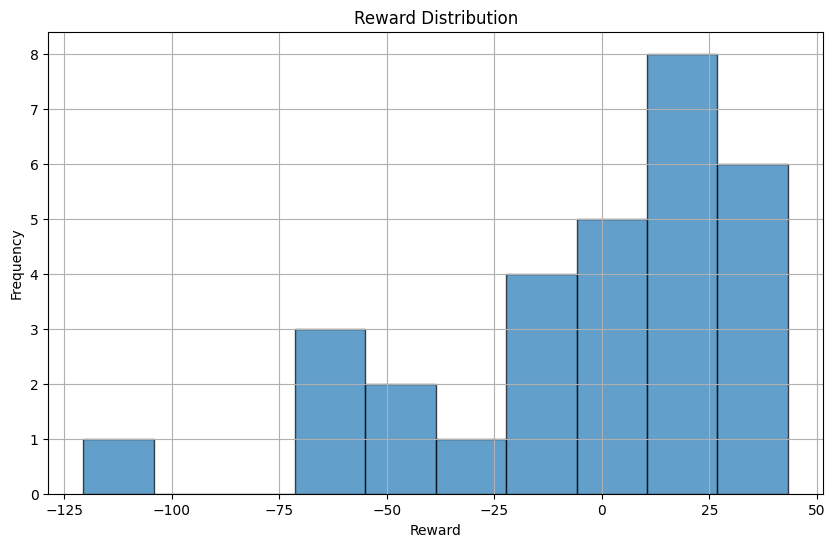
The key findings from the experiments are improvements in total reward, reduction in total distance, elimination of node revisits, and reward distribution. First, the agent’s performance improved significantly over time. Starting with an average reward of -50, the model achieved a peak reward of 43.3 in optimized routes. Additionally, the total distance was reduced: the initial random route had a total travel distance of 200 units, yet after training, the optimized routes reduced the distance to 127 units. In regard to node revisits, initially, the agent revisited nodes multiple times, leading to inefficiencies. However, after training, the model learned to visit each node only once, avoiding redundant trips and reducing unnecessary penalties. Overall, the rewards per episode showed steady improvement as the model learned optimal policies. The reward distribution indicates a positive skew, with high-performing episodes achieving rewards above 30.

The results demonstrate the effectiveness of the GNN-DQN framework in solving the dynamic waste vehicle routing problem. The GNN successfully encoded the spatial relationships within the graph, and the DQN agent efficiently learned to optimize routes through exploration and exploitation, leading to a consistent improvement in travel time. The reduction in total distance and elimination of revisits signify lower fuel consumption, reduced travel time, and decreased operational costs for waste collection—practical benefits that can be easily applied in real-life scenarios. The success of the algorithm and the significant improvement in rewards reflect the model’s ability to generalize across episodes and adapt to different graph configurations dynamically.

Discussion and conclusion

The results of this study demonstrate that the GNN-DQN framework is highly effective in solving the dynamic vehicle routing problem for waste collection. By leveraging Graph Neural Networks to process graph-structured city road data and Deep Q-Networks for decision-making, the model successfully minimized travel distance, avoided revisits, and achieved efficient routing. This approach significantly reduces operational costs, fuel consumption, and carbon emissions, making it a promising solution for smart city applications. For future work, the model can be extended to adapt to dynamic traffic conditions, road conditions, and real-time updates. Additionally, integrating multiple vehicles and optimizing load capacities could further enhance scalability and efficiency in larger urban environments.

References

1. Hauser, H.-E., & Blumenthal, K. (2016). Each Person in the EU Generated 475 kg of Municipal Waste in 2014. Eurostat Press, 56/2016.
2. Jouhara, H., Czajczyńska, D., Ghazal, H., Krzyżyńska, R., Anguilano, L., Reynolds, A. J., & Spencer, N. (2017). Municipal Waste Management Systems for Domestic Use. Energy, 139, 485–506. https://doi.org/10.1016/j.energy.2017.07.162
3. Pichtel, J. (2014). Waste Management Practices (2nd ed.): Municipal, Hazardous, and Industrial. Boca Raton: Taylor & Francis Group.
4. Liang, Y. C., Minanda, V., & Gunawan, A. (2022). Waste Collection Routing Problem: A Mini-Review of Recent Heuristic Approaches and Applications. Waste Management & Research, 40(5), 519–537.
5. Norhafezah, K., Nurfadzliana, A., & Megawati, O. (2017). Simulation of Municipal Solid Waste Route Optimization by Dijkstra’s Algorithm. Journal of Fundamental and Applied Sciences, 9, 732–747.